AIを学んでいくうえでいつか対峙するのが『統計学』。
『え?AIってなんか難しそうなプログラミングするだけじゃないの?』と思う方もいるかもしれませんが、『統計学』と『AI』には切っても切れない固~い関係性があるのです。
今回は『AIと統計学』の関係性について、そして『知っておきたい統計学の基礎』をざっくり解説していきます!
そもそも統計学って?
『そもそも『統計学』ってのを知らんぞ!』という方もいるでしょう。私もはじめはそうでした。
統計学とは『現実世界の様々なデータから数学的な手法を用いてデータの性質や規則性を見つける』ことを目的とした学問のことです。
統計学は日常生活でも使われていて、例えば…。
テレビ番組の視聴率はランダムに選ばれた家からテレビがついているか・どこのチャンネルを付けているかを計測し、番組の視聴率を計算していますし、
天気予報は天気出現率という過去に起きた気象が出現する確率を元にした情報を使い雨などの確率を導き出しています。
統計学の中でも代表的なものは平均値や最大値などで、これらは基本統計量や代表値と呼ばれていて、統計学の考え方や手法を用いてデータの中から見つけ出した情報を意思決定などに用いることを『データ分析(データ解析)』といいます。

統計分析で使うとんでもない量のデータのことを『ビックデータ』と呼ぶそうです。
みんなどこかで聞いたことあるはず。
ちなみに似たようなもので『データサイエンス』というものがありますがこちらは、統計学に情報工学や数学などの様々な手法を組み合わせてデータを分析する分野のことです。
AIと統計学の関係性って?
統計学についてはなんとなく理解できたでしょうか?
『じゃあなんでAIを学ぶ上で統計学が必要なのか』というと…
『学習や予測の際に統計学の考え方を使用しているから』です。
例えば機械学習をするとき。
機械学習はデータをもとにしてどんな傾向やパターンがあるかを学習しますが…
その学習用のデータにどんな特徴があるのか、そのデータの全体はどんな風になっているのか…。
こういったものを機械学習で学習・予測する際のコンピューターの考え方(アルゴリズムといいます)に『統計学』が大きく関わっているのです。
他にも学習したAIモデルがどれほど正確なのかを評価する時にも『統計学』は使われています。
つまり、AIと統計学は切っても切れないズブズブの関係ってことです。
統計学の超基本、基本統計量
では、統計学の最も基礎的な知識である基本統計量についてみてみましょうか。
代表的な基本統計量は以下の通りです。
| 平均値 | データ集合の中心的な値(データの総和を個数で割ったもの) |
| 中央値 | データ集合の中央に位置する値 |
| 最大値 | データ集合で一番大きい値 |
| 最小値 | データ集合で一番小さい値 |
| 分散 | データ集合のばらつきを表す指標 |
| 標準偏差 | データ集合のばらつきを表す指標 |
| 相関係数 | 2項目の関係性の強さの指標 |
このうち平均値や中央値など中心的な位置を示すものを代表値、分散や標準偏差などのデータのばらつきを示すもののことを散布度と呼びます。
基本統計量について一部、詳しく見ていきましょう。
平均値とはデータの値を合計してデータの個数で割ったもののことです。
小学校で必ず通るものなので知ってる人も多いのではないでしょうか?
例えばここに5人分のテストの結果があるとします。
| 点数 | 73 | 65 | 80 | 59 | 64 |
このテストの点数の平均は以下の通りになります。
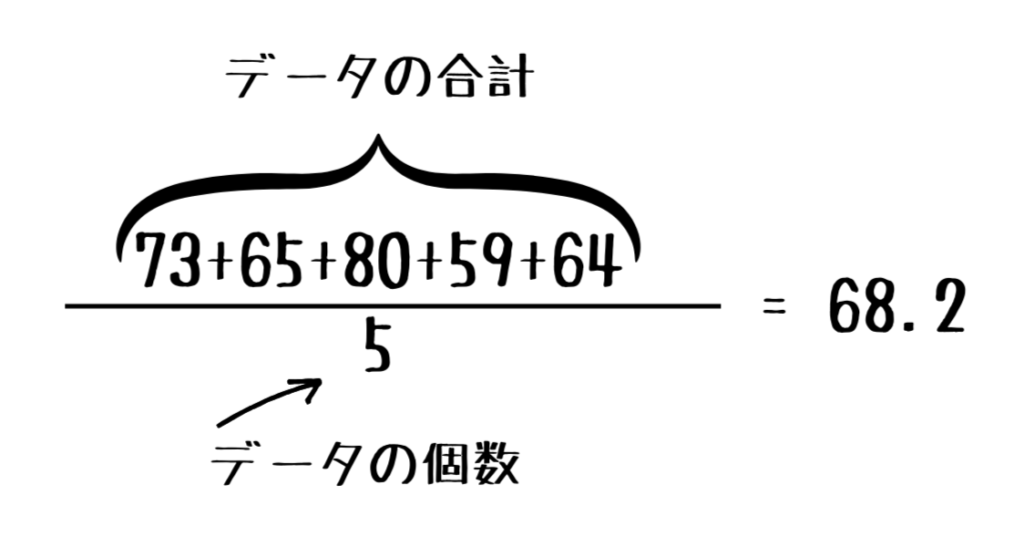
このようにデータの値を合計してデータの個数で割ったものが平均値です。
平均値はデータのすべての値を足しているのでデータ全体の大体の大きさ・傾向をつかむことができます。
中央値とはデータを昇順(小さい順)に並べた時に、ちょうど真ん中に位置する値のことを指します。
| 点数 | 59 | 64 | 65 | 73 | 80 |
平均値の時に使った5人分のテスト結果を点数が低い順に並べ替えました。
この時にちょうど順番が真ん中に来ている値、『65』がテスト結果の中央値だといえます。

ちなみにデータの数が偶数の場合、真ん中がないやんけ!と思いますが、
偶数の場合は真ん中2つの値の平均を中央値として扱います。
中央値は平均値と『真ん中あたりの値を出す』という点が似ています。
『じゃあ中央値なんてどこで使うんだ?』と考える方がいるかもしれません。
中央値の強みはズバリ、『外れ値の影響を受けない』ことです。
外れ値とは…
対象となるデータの中で明らかにに他の値と比べて明らかに大きすぎる・小さすぎる値のことです。
例えば…
| 点数 | 250 | 300 | 350 | 400 | 600 | 800 | 2200 |
このようなデータがあるとすれば異様に高い数値である『2200』が外れ値といえますネ。
平均値はこの外れ値の影響を大きく受けてしまいます。
先ほどのデータの平均値を計算すると『700』となります。
実際に多いのは300~400辺りなのに外れ値に影響されて700辺りが平均だと示しています。
このように外れ値が存在すると平均値はその影響を大きく受けてしまい、データの集まりの真ん中の値を求める指標としては不適切な値になってしまいます。
しかし、中央値は『データ集合のちょうど真ん中』を示すので外れ値の影響を受けないのです。
これが中央値の『強み』です。

データを昇順に並べた際、中央値から分けて下半分の中央値(全体の25%の値)を第一四分位数、上半分の中央値(全体の75%の値)のことを第三四分位数と呼びます。
後ほどのグラフ解説で出てくるのでちょっと覚えててください。
分散はデータの集まりがばらついているか、ある一点の付近に集中しているかなどのばらつき具合を表現する数値指標のことです。
ざっくり(ホントにざっくりです)いうと、『データが平均値と比べてどの程度近いか』を表した数値、ということです。
分散の計算ははっきり言ってやることが多いです。
中央値で使用した表をもとに分散の計算を解説しますね。
| 点数 | 250 | 300 | 350 | 400 | 600 | 800 | 2200 |
平均値を計算しましょう。
その前に…今回はわかりやすくするために、外れ値である『2200』を除いたデータで平均値を計算しましょう。
データの平均値は『450』です。
平均を計算したら、次は各データを平均値で引いたもの(偏差と言います)を計算しましょう。

この偏差が0に近ければ近いほど平均値に近い値だ、ということです。
さて、各データがどれほど平均値から離れているかは偏差を出すことでわかりました。
分散は『データ全体がどれほど平均値から離れているか』を表しているので、偏差の平均値を計算すればいいわけですが…。
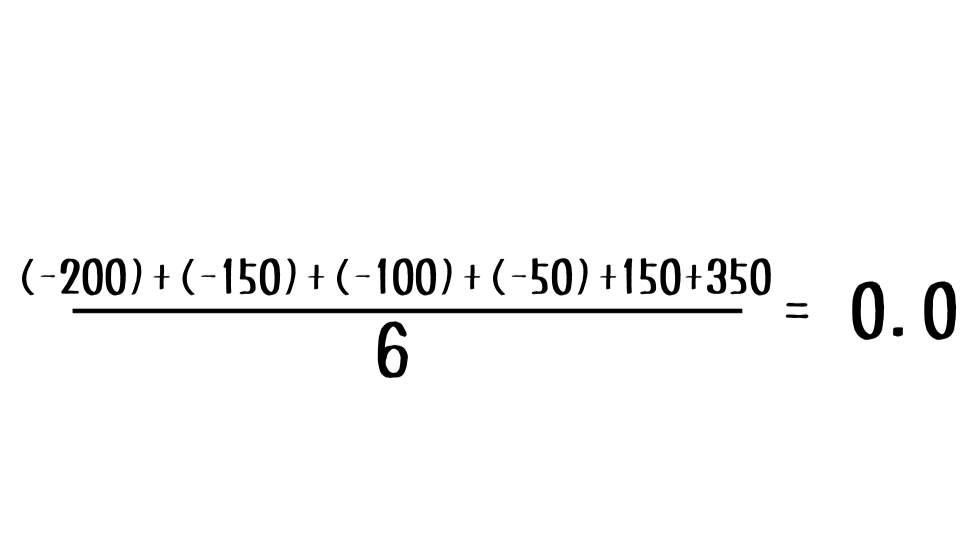
このまま計算するとなぜか0になってしまいます。
これは偏差のプラスの値とマイナスの値が足し合わせた時に互いを打ち消しあってしまうためです。
ではどうすればいいのか?マイナスを消せばいいのです。
マイナスを消すためには値を2乗します。
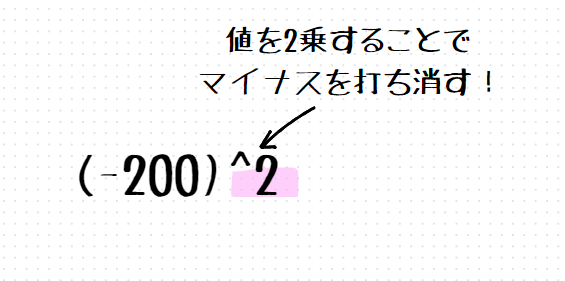
それぞれの偏差を2乗したもので平均を計算することで、分散を求めることができます。

この『36,666.66…』という値がこのデータの分散です。
データ同士の分散を比べることで、どちらのデータの集まりがよりばらついているかを見ることができます。
標準偏差とは分散と同じく、データのばらつきを表す指標のことです。
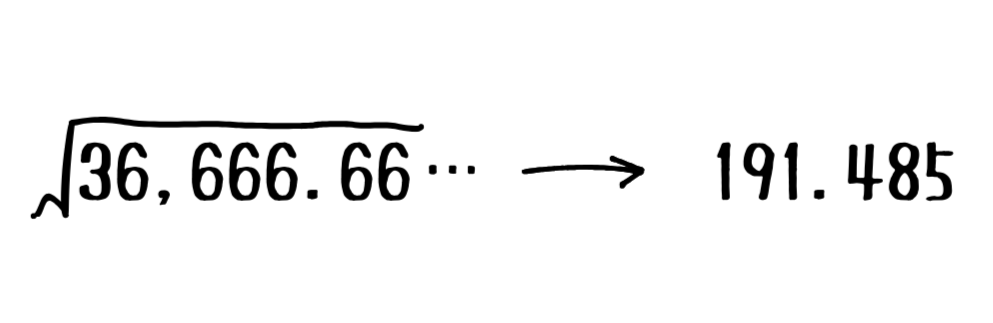
標準偏差は先ほど計算した分散から平方根を取ることで計算できます。

こういうことですね。
…さっき計算した分散の値、大きすぎてわかりにくいですよね?
これは値を2乗してしまったので、元のデータの値から大きく変わってしまったのです。
標準偏差は『分散から平方根を取って、元に戻してわかりやすくしよう!!』ということですネ。
『わかりにくいだけだったら別に標準偏差にする必要なんてないんじゃないか?』と思った方もいると思います。
実は分散をしてしまうと『単位』が変わってしまうのです。
例えば、長さの単位は『cm』ですよね?
この長さを分散を計算するために2乗してしまうと、単位が面積(㎠)になってしまうのです。(長さ×長さ = 面積、ということです)
面積と長さでは意味合いが大きく変わってしまいます。
標準偏差は分散を平方根を取っている、つまり単位をもとに戻しているので、この『分散で単位が変わってしまう』問題を解決できるとても便利な指標ということです。
相関係数は2つのデータの関係性を測る統計指標のことです。
相関係数には以下のような特徴があります。
- 必ず-1以上+1以下の値である
- 正の相関が強いほど相関係数は+1に近づく
- 負の相関が強いほど相関係数は-1に近づく
ここで出てきた『正の相関』・『負の相関』とは『データ同士の関連性』のことを指します。
グラフにするとわかりやすいですね。
『正の相関』は横軸(x)の値が増えると縦軸(y)の値も増えるということを指す言葉で…
反対に『負の相関』は横軸(x)の値が増えると縦軸(y)の値が減るということを指す言葉です。
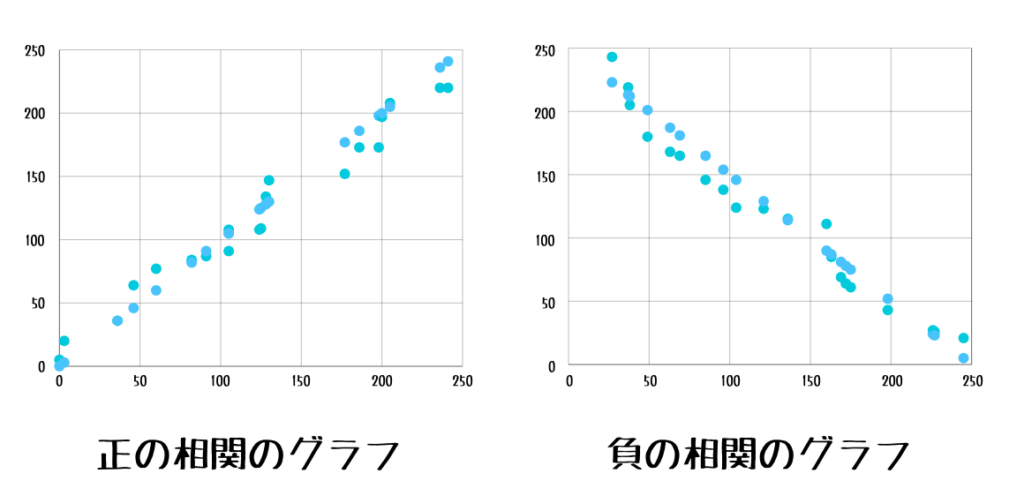
正の相関はグラフが右肩上がりになり、負の相関の時はグラフは右肩下がりになる、ということですネ。
また、正(または負)の相関が強いということは、『グラフがきれいな直線に近い』ということを指します。
学校の数学でよく聞いた『比例の関係』は相関係数が±1に近いものですね。

ちなみに相関係数が0に近いとグラフは右肩上がりでも右肩下がりでもないとっ散らかったものになります。
つまり、縦軸と横軸の2つのデータ間には関係性がない、ということが分かりますね。
統計学でよく出てくるグラフの種類
さて、統計で出てくる『基本統計量』についてはなんとなくわかったでしょうか。
統計によるデータ分析ではグラフによる可視化というものをします。
図に表すことでパッと見てデータ間にどんな関係があるのか・どんな傾向があるのかなどが分かるのです。
統計でよく使われるグラフには『ヒストグラム』『棒グラフ』『折れ線グラフ』『散布図』『箱ひげ図』があります。
順番に見ていきましょうか。
ヒストグラムとは数値のデータ集合に対して『この範囲の値が何個出てきたか』を分けて棒状のグラフにしたものです。
『0~5までの値』、『6~10までの値』…のようにある適度の区間で区切って集計している、というイメージです。
この区間のことを『階級(bin)』と呼び、グラフの高さのことを『度数』と呼びます。
ヒストグラムを全体見ることで、『この区間(度数)にデータが集まってるんだな。』と、データ全体の分布度合いや内訳を知ることができるのです。
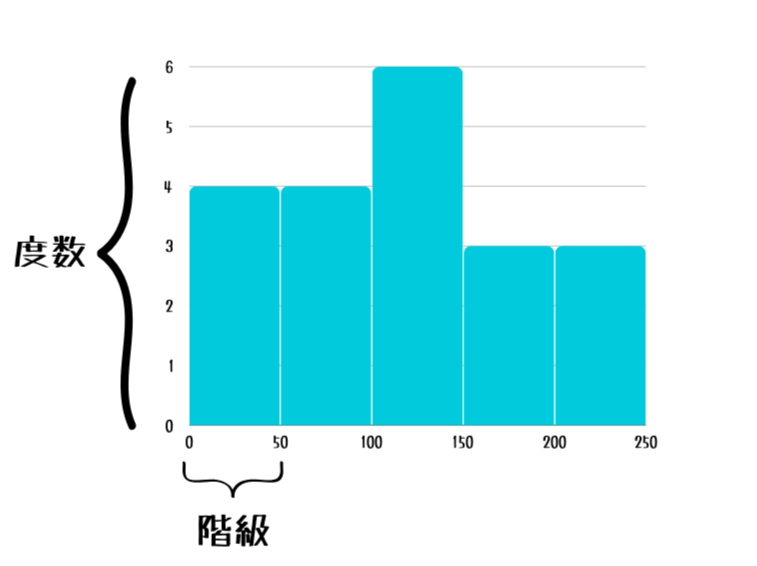
こちらはみなさんご存じですよね。
ただ先ほど紹介したヒストグラムを見てこう思った人もいるんじゃないでしょうか?
『ヒストグラムって棒グラフと一緒じゃね??』って…。
実は結構違います。ホントに。
棒グラフはそれぞれの棒が独立しており、棒同士の値の大小を比べることが目的です。
それに対してヒストグラムは『グラフ全体』を見て『データの分布』を見ることが目的です。
ヒストグラムは縦・横軸が表すものやグラフの目的がはっきりしているんですね。
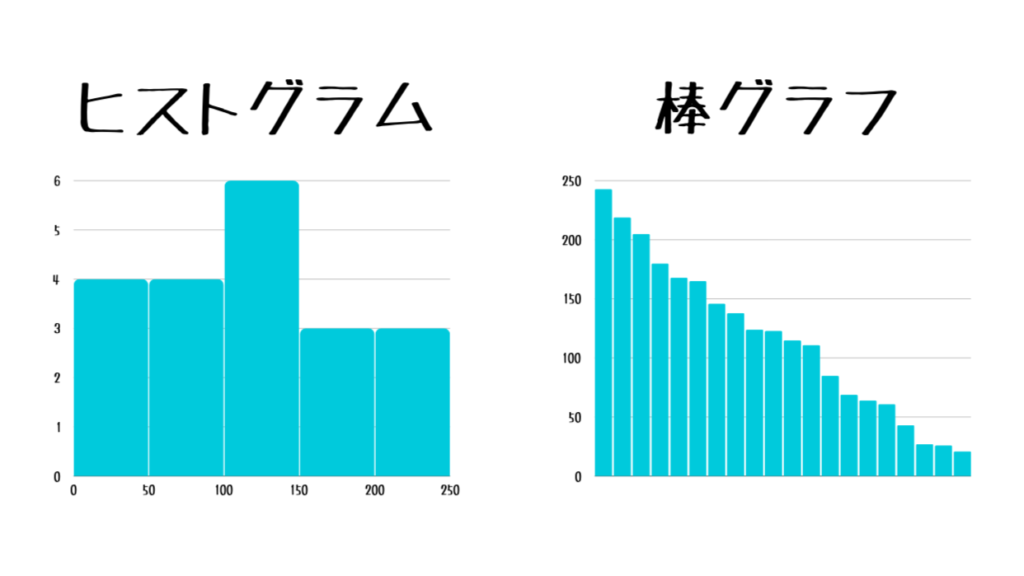
これが棒グラフとの大きな違いです。
これも多分よく見たことあると思います。
数などの大きさを表すグラフの点を線で結んだもののことを『折れ線グラフ』と呼びます。
具体的には時系列(時間によって変化するデータ)を扱う際によく使います。
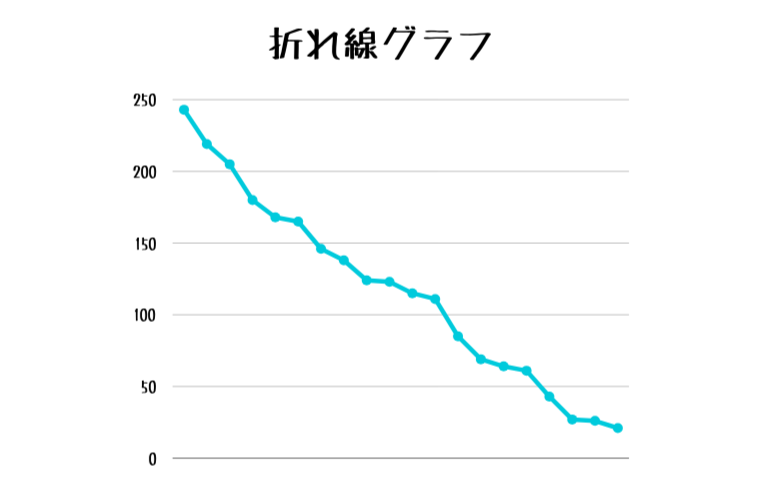
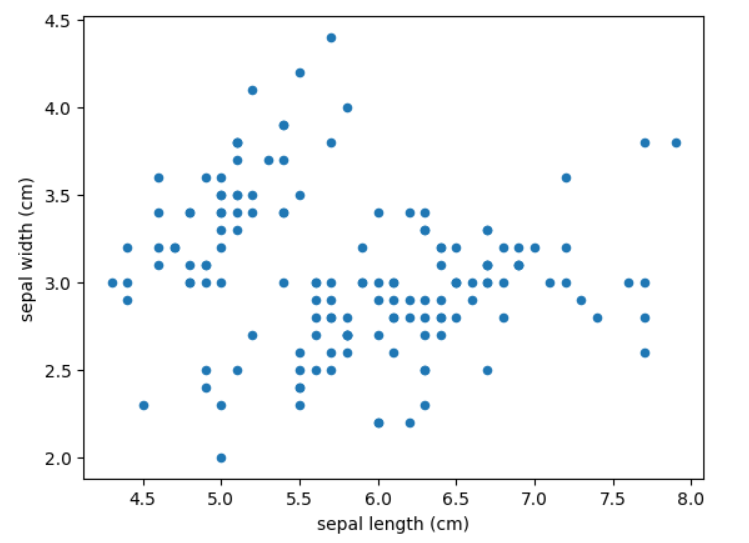
散布図は縦軸と横軸、2つの項目の中で1つ1つのデータがどこに位置するのかを点で表したグラフのことです。
つまり2つの項目の相関を見るためのグラフ、ということです。
相関係数の項目で使っていたグラフが『散布図』ですね。
箱ひげ図は中央値や第1四分位数、第3四分位数が一目でわかるグラフのことです。
このグラフを見ることでデータの分布をすぐに知ることができます。すごいグラフなんです。

箱ひげ図はこのようなグラフで表されます。
この箱の部分の真ん中にある線が『中央値』、箱の下底が『第一四分位数』、上底が『第三四分位数』です。
箱の上にある線(これが『ひげ』です。)が『最大値』を表し、箱の下の線が『最小値』を表しています。
ひげの長さがデータの範囲を表しているのです。

ものによってですが、平均値や外れ値が入っている箱ひげ図もあります。
平均値はバツ印などの記号で表されていて…
外れ値はひげの外側に出ているので多分一目でわかります。多分ね。
まとめ
今回はAIを学ぶ上で大切な統計学のお話でした。
- 統計学とはデータからデータの性質や規則性を見つける学問のこと
- AIは学習や予測の際に統計学を用いている
- 基本統計量には平均値や中央値などの代表値、分散や標準偏差などの散布度がある
- 統計でよく使われるグラフには『ヒストグラム』『棒グラフ』『折れ線グラフ』『散布図』『箱ひげ図』がある
AIは大量のデータで出来ているので、データを正しく見るために統計学が必要なんだ、ということが理解できれば大丈夫です。
 NANIMONO
NANIMONO 
